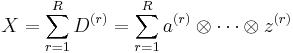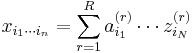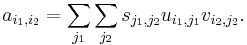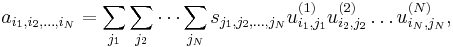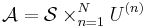Higher-order singular value decomposition

In multilinear algebra, there does not exist a general decomposition method for multi-way arrays (also known as N-arrays, higher-order arrays, or data-tensors) with all the properties of a matrix singular value decomposition (SVD). A matrix SVD simultaneously computes

(a) a rank-R decomposition and

(b) the orthonormal row/column matrices.

These two properties can be captured separately by two different decompositions for multi-way arrays.

Property (a) is extended to higher order by a class of closely related constructions known collectively as CP decomposition (named after the two most popular and general variants, CANDECOMP and PARAFAC). Such decompositions represent a tensor as the sum of the n-fold outter products of rank-1 tensors, where n is the dimension of the tensor indices.

Property (b) is extended to higher order by a class of methods known variably as Tucker3, N-mode SVD, and N-mode principal component analysis (PCA). (This article will use the general term "Tucker decomposition".) These methods compute the othonormal spaces associated with the different axes (or modes) of a tensor. The Tucker decomposition is also used in multilinear subspace learning as multilinear principal component analysis. This terminology was coined by P. Kroonenberg in the 1980s, but it was later called multilinear SVD and HOSVD (higher-order SVD) by L. De Lathauwer.

Historically, much of the interest in higher-order SVDs was driven by the need to analyze empirical data, especial in psychometrics and chemometrics. As such, many of the methods have been independently invented several times, often with subtle variations, leading to a confusing literature. Abstract and general mathematical theorems are rare (though see Kruskal^[1] with regard to the CP decomposition); instead, the methods are often designed for analyzing specific data types. The 2008 review article by Kolda and Bader^[2] provides a compact summary of the history of these decompositions, and many references for further reading.

1 CP decomposition
- 1.1 Definition
2 Tucker decomposition
3 Applications
4 References

CP decomposition

Main article: CP decomposition

Definition

A CP decomposition of an N-way array X, with elements 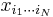$x_{i_1 \cdots i_N}$ , is

$X = \sum_{r=1}^{R} D^{(r)} = \sum_{r=1}^{R} a^{(r)} \otimes \cdots \otimes z^{(r)}$

where $\otimes$ denotes the tensor product. The r tensors 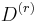$D^{(r)}$ (known as simple tensors, rank-1 tensors, dyads, or, in quantum mechanics, product states) are constructed from the rN vectors $a^{(r)}, \cdots, z^{(r)}$ . With indices, this is

$x_{i_1 \cdots i_n} = \sum_{r=1}^{R} a^{(r)}_{i_1} \cdots z^{(r)}_{i_N}$

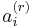where $a^{(r)}_{i}$ is the i-th element of the vector 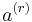$a^{(r)}$ , etc.

Tucker decomposition

Main article: Tucker decomposition

History

In 1966, L. Tucker proposed a decomposition method for 3-way arrays (inappropriately referred to as a 3-mode "tensors") as a multidimensional extension of factor analysis.^[3] This decomposition was further developed in the 1980s by P. Kroonenberg, who coined the terms Tucker3, Tucker3ALS (an alternating least squares dimensionality reduction algorithm), 3-Mode SVD, and 3-Mode PCA.^[4] In the intervening years, several authors developed the decomposition for N-way arrays. Most recently, this work was treated in an elegant fashion and introduced to the SIAM community by L. De Lathauwer et al. who referred to the decomposition as an N-way SVD, multilinear SVD and HOSVD.^[5]

Definitions

Let the SVD of a real matrix be 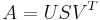$A = U S V^T$ , then it can be written in an elementwise form as

$a_{i_1,i_2} = \sum_{j_1} \sum_{j_2} s_{j_1,j_2} u_{i_1,j_1} v_{i_2,j_2}.$

$U$ and $V$ give, in a certain sense optimal, orthonormal basis for the column and row space, $S$ is diagonal with decreasing elements. N-mode SVD can be defined by the multidimensional generalization of this concept:

$a_{i_1,i_2,\dots,i_N} = \sum_{j_1} \sum_{j_2}\cdots \sum_{j_N} s_{j_1,j_2,\dots,j_N} u^{(1)}_{i_1,j_1} u^{(2)}_{i_2,j_2} \dots u^{(N)}_{i_N,j_N},$

where the $U^{(n)} = [u^{(n)}_{i,j}]_{I_n \times I_n}$ matrices and the $\mathcal{S} = [s_{j_1,\dots,j_N}]_{I_1 \times I_2 \times \cdots \times I_N}$ core tensor should satisfy certain requirements (similar ones to the matrix SVD), namely

Each 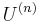$U^{(n)}$ is an orthogonal matrix (called n-mode singular matrix).
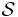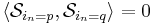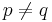Two subtensors of the core tensor $\mathcal{S}$ are orthogonal i.e., $\langle\mathcal{S}_{i_n = p}, \mathcal{S}_{i_n = q}\rangle = 0$ if $p \neq q$ .
The subtensors in the core tensor 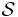$\mathcal{S}$ are ordered according to their Frobenius norm, i.e. 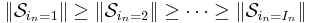$\|\mathcal{S}_{i_n = 1}\| \geq \|\mathcal{S}_{i_n = 2}\| \geq \dots \geq \|\mathcal{S}_{i_n = I_n}\|$ for n = 1, ..., N.

Notation:

$\mathcal{A} = \mathcal{S} \times_{n=1}^N U^{(n)}$

Algorithm

Tensor SVD can be built on SVD as follows:^[6]

Given a tensor, T of shape 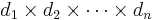$d_1\times d_2\times\cdots\times d_n$ , the i^th singular tensor is given by making a matrix,

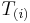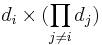$T_{(i)}$ , the $d_i\times (\prod _{j \neq i} d_j)$ matrix corresponding to $T$ .

taking its left singular vectors, 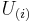$U_{(i)}$ .

The core tensor is then the tensor product of those 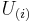$U_{(i)}$ s.

Applications

Main applications are extracting relevant information from multi-way arrays. Used in factor analysis, face recognition (TensorFaces), human motion analysis and synthesis, and many other signal processing endeavours, such as Genomic Signal Processing.^[7]^[8]^[9]

It is also used in tensor product model transformation-based controller design. In multilinear subspace learning^[10], it is modified to multilinear principal component analysis^[11] for gait recognition.

References

^ Kruskal, J. B. (1989). "Rank, decomposition, and uniqueness for 3-way and N-way arrays". In R. Coppi & S. Bolasco (Eds.), Multiway data analysis (pp. 7-18). Amsterdam: Elsevier. [ PDF ].
^ Tamara G. Kolda and Brett W. Bader, "Tensor Decompositions and Applications," SIAM Rev. 51, pp. 455-500 (46 pages). [ PDF ].
^ Ledyard R. Tucker (September 1966). "Some mathematical notes on three-mode factor analysis". Psychometrika 31 (3): 279–311. doi:10.1007/BF02289464.
^ P. M. Kroonenberg (1983). "Three-mode principal component analysis: Theory and applications". DSWO Press, Leiden. http://three-mode.leidenuniv.nl/bibliogr/kroonenbergpm_thesis/index.html.
^ Lieven De Lathauwer, Bart De Moor and Joos Vandewalle (April 2000). "A multilinear Singular Value Decomposition". SIAM 21 (4). http://perso-etis.ensea.fr/~lathauwer/ldl-94-31.pdf.
^ Vasilescu et al. "TensorTextures: Multilinear Image-Based Rendering", SIGGRAPH 2004
^ L. Omberg, G. H. Golub and O. Alter (November 2007). "A Tensor Higher-Order Singular Value Decomposition for Integrative Analysis of DNA Microarray Data From Different Studies". PNAS 104 (47): 18371–18376. doi:10.1073/pnas.0709146104.
^ L. Omberg, J. R. Meyerson, K. Kobayashi, L. S. Drury, J. F. X. Diffley and O. Alter (October 2009). "Global Effects of DNA Replication and DNA Replication Origin Activity on Eukaryotic Gene Expression". Molecular Systems Biology 5 (1): 312. doi:10.1038/msb.2009.70.
^ C. Muralidhara, A. M. Gross, R. R. Gutell and O. Alter (April 2011). "Tensor Decomposition Reveals Concurrent Evolutionary Convergences and Divergences and Correlations with Structural Motifs in Ribosomal RNA". Public Library of Science (PLoS) One 6 (4): e18768. doi:10.1371/journal.pone.0018768.
^ Haiping Lu, K.N. Plataniotis and A.N. Venetsanopoulos, "A Survey of Multilinear Subspace Learning for Tensor Data", Pattern Recognition, Vol. 44, No. 7, pp. 1540–1551, Jul. 2011.
^ H. Lu, K. N. Plataniotis, and A. N. Venetsanopoulos, "MPCA: Multilinear principal component analysis of tensor objects," IEEE Trans. Neural Netw., vol. 19, no. 1, pp. 18–39, Jan. 2008.